こんにちは、プロオンライン家庭教師の「めじろ」です♪
食塩水の問題を一発で解けるようにする方法(小学生・中学受験用)を説明します。
- 説明を何回聞いても覚えられない
- 動画を見ても実践で使えなかった
という方は、この記事で攻略可能です!
ぜひ最後までご覧ください。
食塩水の問題の解き方で覚えるべき公式はこれだけ!
食塩水の問題の解き方を、理屈や数直線で示す先生がいますが、算数が苦手な子は、まず公式を使って解いてみるところからスタートしましょう!
私の教え子でも、最初は基本問題すら「?」だった子が、応用問題まで自力で解けるようになりました♪
まずはカッコつけず、公式を覚えて使ってOKなんです。
【食塩水の公式】
- 食塩(g)×濃度=食塩の量(g)
- 食塩(g)÷濃度=食塩水の量(g)
- 食塩(g)÷食塩水の量(g)=濃度
ただ、これだと覚えにくいですよね?
私は、覚えられないです!笑
そういう方は、こちらがおすすめ↓
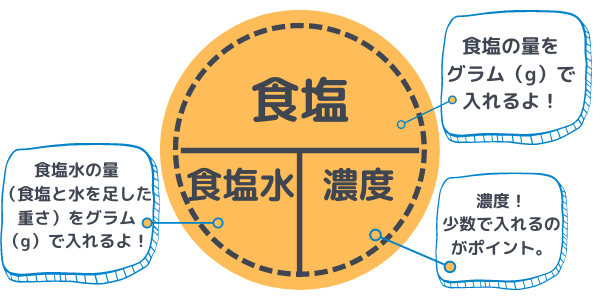
ポイントは、「食塩」と「食塩水」は、重さ=グラム(g)で入れることと、濃度は%ではなく少数(4%なら0.04)で入れるということだけ!

ちょうど、速さの問題ででてくる「み(き)・は・じ」と同じように、タテは割り算、ヨコは掛け算だと思ってくださいね。
食塩水の基本問題の解き方【クリアしておきたい5パターン】
実際に問題を解いてみましょう!
食塩水の問題「入っている食塩の量は何gですか」の解き方
【問い】5%の食塩水が100gあります。ここに入っている食塩は何gですか。
【考え方】
上記の公式に当てはめます。
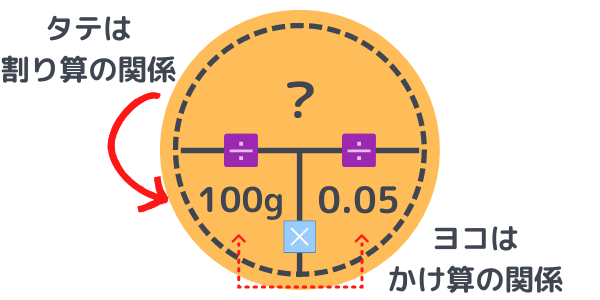
図から、
100×0.05=?
⇒ 100×0.05=5 → (答え)食塩は5g
簡単に出せますね!
食塩水の問題「できる食塩水の量は何gですか」の解き方
【問い】20gの食塩を使って、4%になるように食塩水を作ります。できる食塩水の量は何gですか。
【考え方】
公式に当てはめます。
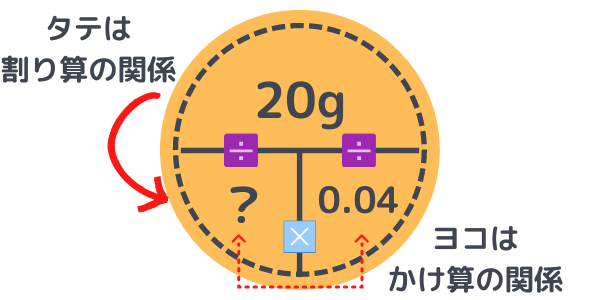
図から、
20÷0.04=?
⇒ 20÷0.04=500 → (答え)できる食塩水は500g
食塩水の問題「○%の食塩水を作るには水は何g必要ですか」の解き方
【問い】50gの食塩を使って4%になるように食塩水を作るには、水は何g必要ですか。
【考え方】
ん?と思ってしまうかもしれませんが、これも実は簡単です。
まずは、公式にあてはめます。
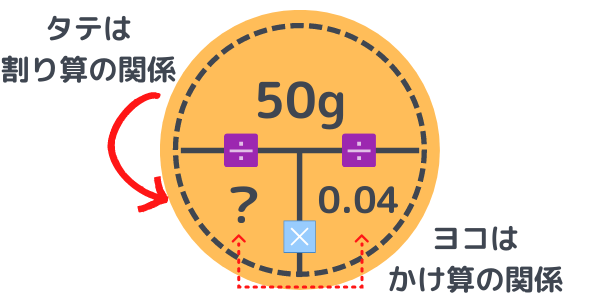
図から、
50÷0.04=?
⇒ 50÷0.04=1250 → できる食塩水は1250g
ということは、食塩の量は50gだと分かっているので、必要な水の量は
1250g - 50g = 1200 (答え)必要な水の量は1200g
まず食塩水全体の重さを求めて、そこから食塩の重さを引けばいいんですね!
食塩水の問題「食塩水の濃度は何%になりますか」の解き方
【問い】45gの食塩と400gの水を混ぜて食塩水を作ります。濃度は何%になりますか。
【考え方】
これは、公式に当てはめるだけでできます。
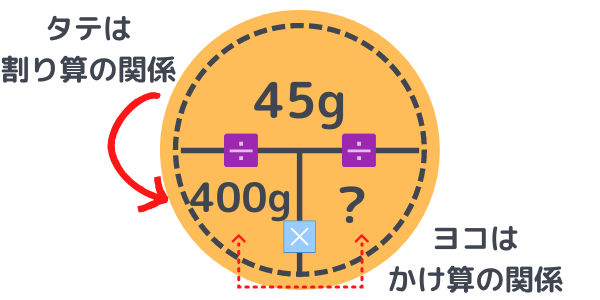
図から、
45÷400g=?
⇒ 45÷400g=0.1125 → (答え)【0.1125を百分率になおして】11.25%
食塩水の問題「2つの食塩水を混ぜると何%の食塩水になりますか」の解き方
【問い】10%の食塩水Aを100gと、2%の食塩水B300gを混ぜると、何%の食塩水になりますか。
【考え方】
2つも食塩水が出てくるからといって、焦ってはいけません。公式を知っていれば、誰でもできますよ!
まずは、それぞれの食塩の量を求めます。
A(10%の食塩水100g)の食塩の量は、公式に当てはめると、
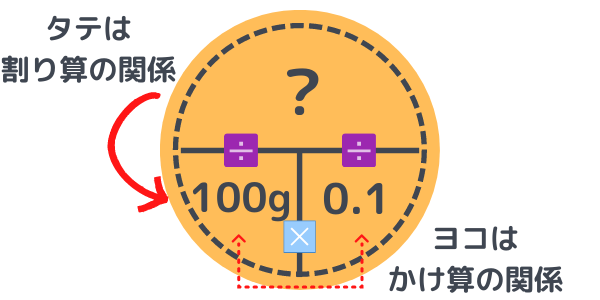
100g×0.1=10g ⇒ Aの食塩は10g
B(2%の食塩水300g)の食塩の量は、公式に当てはめると、
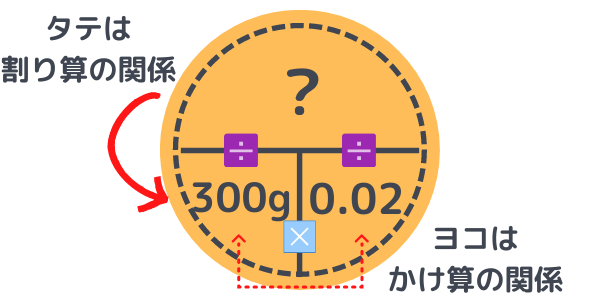
300g×0.02=6g ⇒ Bの食塩は6g
ここまで分かったら、次はAとB二つの食塩水の情報を合わせて、濃度を計算していきます!
公式にあてはめるとき、AとBの数字を足せばいいだけなので、カンタンです。
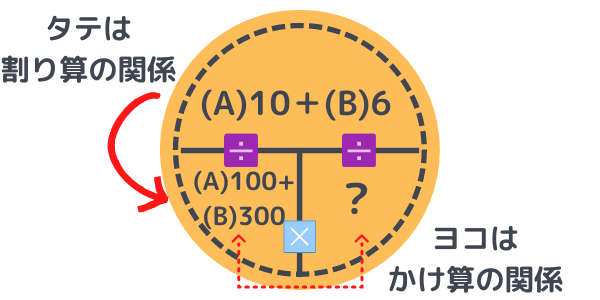
式としては、
(10+6)÷(100+300)=?
⇒16÷400=0.04 (答え)AとBを合わせた食塩水の濃度は4%
すでにある食塩水に「食塩水・水・食塩を加える(蒸発させる)」問題の解き方【中学受験生は必須】
ここから先は、少し応用編となります。
上の基本問題がなんとなくわかったよ!という人から、チャレンジしてみてください♪
食塩水の問題「□%の食塩水にするには何gの水を加える(蒸発させる)とよいですか」の解き方
【問い】5%の食塩水600gがあります。ここに水を加えて3%の食塩水にするには、何gの水を加えるとよいですか。
【考え方】
まずは、分かっている数字を公式にあてはめてみます。
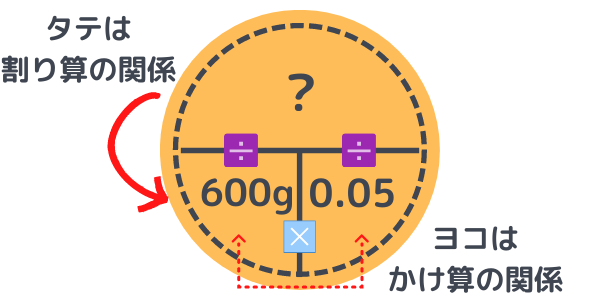
すると、
600g×0.05g=30g
もとの食塩の量は30gということがわかります。
ここまできたら、目指している【3%の食塩水】の公式を書いてみます。
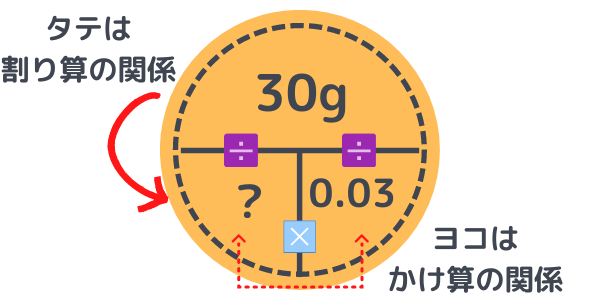
ここでポイントとなるのは、食塩の量(30g)は、目指している【3%の食塩水】でも同じということです。
今回は水を足すだけなので、食塩は元の量のまま変わらないんですね。
上記を計算すると、
30÷0.03=1000g
最終的にできる食塩水の量は、1000gだということがわかりました。
問題文には、もとの食塩水は600gとありますので、
1000-600=400g (答え)追加する水の量は400g
※水を足すのではなく、蒸発させる問題の場合も、【もとの食塩水の量】と【目指す食塩水の量】の差を求めるやり方は同じです。
蒸発させる場合、【目指す食塩水の量】の方がより少なくなりますが、引き算で差を求めれば、何g蒸発させればいいのか分かりますね。
「え、蒸発させるの…?!」ってビックリしてしまうかもしれませんが、落ち着いてやれば、絶対に解けますよ!
食塩水の問題「AとB、2つの食塩水混ぜたら○%になった。Bの食塩水は何g混ぜたでしょう」の解き方
ここで、少し別のやり方をお教えします。
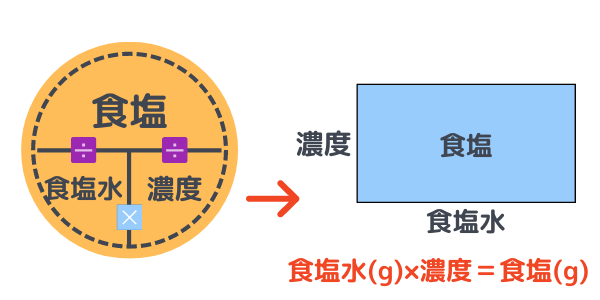
下の図のように、食塩水の公式は、四角形の面積の公式にも当てはめることができます。
タテを濃度、ヨコを食塩水にすれば、
濃度×食塩水の量 = 食塩の量
という公式が誕生します。
こちらの方が解きやすい問題もあります。
例えば、以下のような問題です。練習してみましょう。
【問い】3%の食塩水Aを300gと、20%の食塩水Bを混ぜて、8%の食塩水を作りたいです。食塩水Bは、何g混ぜたらよいですか。
- ちょっとまって、何からやったらいいの…?
- 全くもって検討つかない(泣)
という方がほとんどかもしれませんが、さきほどの四角を使えば、解けちゃいます♪
【考え方】
まず、AとBの四角形バージョンの公式を、ならべて書きます。
濃度の関係で、AよりもBのほうが、タテが長くなりますね。

そのあと、目指す【8%の食塩水】を書きます。
オレンジの部分が、【8%の食塩水】です。

ただ、このままだと四角形の公式が使えないので、ちょっとだけ、工夫します。

図のとおり、(あ)の部分を、(い)の部分にピッタリ当てはめることができれば、公式を成立させることができます。
そのために、(あ)=(い)となるような、「?」の値を求めましょう!
(あ)の面積は、0.05 × 300g = 15なので、
(い)の面積は、0.12 × ? =15
⇒ ?=15 ÷ 0.12
⇒ ?=125
【問い】に戻ってみると、
3%の食塩水Aを300gと、20%の食塩水Bを混ぜて、8%の食塩水を作りたいです。食塩水Bは、何g混ぜたらよいですか。
だったので、答えは125gになります。
…どうでしたか?
最後の問題は、なかなか最初からスラスラ解くのは難しいかもしれませんが、練習してみてくださいね!
特に、中学受験をする子は、苦手なところを放置してしまうと、あとあと大変ですので、公式を使ってラクに習得することがおすすめです。
私も、算数がとっても苦手だったので、できない人の気持ちがよく分かります。
このブログでは、また気づいたときに算数の解法などもアップしていきますので、ぜひ活用してくださいね。
なお、やっているうちに「あれ?」とこんがらがってしまったら、まずは分かっている数字をとにかく公式にぶち込んで、手を動かすようにすると良いですよ。
頑張ってください!





